- PostGreSQL(三)PostGIS
- PostGreSQL(四)PostGIS-空间数据存储
- PostGreSQL(五)PostGIS-常用函数
- PostGreSQL(六)PostGIS-空间连接和空间索引
- PostGreSQL(七)PostGIS-几何图形创建函数
- PostGreSQL(八)PostGIS-图形有效性和简单性
- PostGreSQL(九)PostGIS-几何图形的相等
- PostGreSQL(十)PostGIS-最近领域搜索
- PostGreSQL(十一)PostGIS-其他函数
一、PostGIS介绍
PostGIS是一个空间数据库,空间数据库像存储和操作数据库中其他任何对象一样去存储和操作空间对象。
空间数据库将空间数据和对象关系数据库(Object Relational database)完全集成在一起。实现从以GIS为中心向以数据库为中心的转变。
PostGIS通过向PostgreSQL添加对空间数据类型、**空间索引(R-Tree)和空间函数的支持,将PostgreSQL数据库管理系统转换为空间数据库**,可以说PostGIS仅仅只是PostgreSQL的一个插件,但是它将PostgreSQL变成了一个强大的空间数据库!
最重要的只要接触过SQL语言,就可以利用PostGIS的SQL语法便捷的操纵装载着空间信息的数据框(数据表),这些二维表除了被设定了一个特殊的空间地理信息字段(带有空间投影信息、经纬度信息等)之外,与主流数据管理系统所定义的各种字段并无两样。
PostGIS安装不仅依赖于PostgreSQL,还依赖于很多插件:
- GEOS几何对象库
- GDAL栅格功能
- LibXML2
- LIBJSON
PostGIS的特点如下:
- PostGIS支持所有的空间数据类型,这些类型包括:点(POINT)、线(LINESTRING)、面(POLYGON)、多点 (MULTIPOINT)、多线(MULTILINESTRING)、多面(MULTIPOLYGON)和几何集合 (GEOMETRYCOLLECTION)等。PostGIS支持所有的对象表达方法,比如WKT和WKB。
- PostGIS支持所有的数据存取和构造方法,如GeomFromText()、AsBinary(),以及GeometryN()等。
- PostGIS提供简单的空间分析函数(如Area和Length)同时也提供其他一些具有复杂分析功能的函数,比如Distance。
- PostGIS提供了对于元数据的支持,如GEOMETRY_COLUMNS和SPATIAL_REF_SYS。同时,PostGIS也提供了相应的支持函数,如AddGeometryColumn和DropGeometryColumn。
- PostGIS提供了一系列的二元谓词(如Contains、Within、Overlaps和Touches)用于检测空间对象之间的空间关系,同时返回布尔值来表征对象之间符合这个关系。
- PostGIS提供了空间操作符(如Union和Difference)用于空间数据操作。
- 数据库坐标变换
- 球体长度运算
- 三维的几何类型
- 空间聚集函数
- 栅格数据类型
1.1 空间数据类型
- 空间数据类型用于指定图形为点(point)、线(line)和面(polygon)
- 普通数据库拥有字符串(string)、数值(number)和日期(date)这些数据类型,空间数据库添加了额外的数据类型(空间数据类型)以用于表达地理特征(geographic features)。 这些空间数据类型抽象并封装了诸如边界(boundary)和维度(dimension)等空间结构。 在许多方面,空间数据类型可以简单的理解为形状(shape)
1.2 空间索引和边界框
- 多维度空间索引被用于进行空间操作的高效处理(注意是多维度哦,而不是只有针对二维空间数据的索引)
- 由于多边形(Polygon)可以重叠,可以相互包含,并且可以排列在二维(或更多维数)空间中,因此无法使用B树索引有效地索引它们。 空间数据库提供了一个“空间索引(spatial index)”,它回答了“哪些对象在这个特定的边界框内?”这个问题。 边界框(bounding box)是平行于坐标轴且包含给定地理要素(feature)的最小的矩形。
- 空间索引不像B树索引那样提供精确的结果,而是提供近似的结果。
- 各种数据库实际实现的空间索引差异很大,最常见的实现是R-tree(在PostGIS中使用),但在其他空间数据库中也有基于四叉树(Quadtrees)的实现和基于网格的索引(grid-based indexes)的实现
1.3 空间函数
空间函数构建于SQL语言中,用于进行空间属性和空间关系的查询,空间函数中的大部分可以被归纳为以下五类:
- 转换 —— 在geometry(PostGIS中存储空间信息的格式)和外部数据格式之间进行转换的函数
- 管理 —— 管理关于空间表和PostGIS组织的信息的函数
- 检索 —— 检索几何图形的属性和空间信息测量的函数
- 比较 —— 比较两种几何图形的空间关系的函数
- 生成 —— 基于其他几何图形生成新图形的函数
参考: https://zhuanlan.zhihu.com/p/67232451
二、空间数据存储
使用geography这种数据类型时,PostGIS的内部计算是基于实际地球球体来计算的;
而使用geometry这种数据类型时,PostGIS的内部计算是基于平面来计算的。
2.1 几何类型(Geometry Type)
Geometry(几何对象类型)是PG的一个基本存储类型,PostGIS的空间数据都会以Geometry的形式存储在PostgreSQL里,本质是个二进制对象。
2.1.1 OGC的WKB和WKT格式
PostGIS基于OGC的“Simple Feature for Specification for SQL”规范,在Geometry对象上实现了一系列的GIS Object(地物对象),使用了OGC推荐的WKT(Well-Known Text)和WKB(Well-Known Binary)格式进行描述,大幅增加了易用性,例如WKT的7个基本类型:
点:POINT(0 0) 线:LINESTRING(0 0,1 1,1 2) 面(多边形):POLYGON((0 0,4 0,4 4,0 4,0 0)) 简单多边形 POLYGON((0 0,4 0,4 4,0 4,0 0),(1 1, 2 1, 2 2, 1 2,1 1)) 多边形有一个内部的"孔洞(hole)" 多点:MULTIPOINT((0 0),(1 2)) 多线:MULTILINESTRING((0 0,1 1,1 2),(2 3,3 2,5 4)) 多面:MULTIPOLYGON(((0 0,4 0,4 4,0 4,0 0),(1 1,2 1,2 2,1 2,1 1)), ((-1 -1,-1 -2,-2 -2,-2 -1,-1 -1))) 几何集合:GEOMETRYCOLLECTION(POINT(2 3),LINESTRING(2 3,3 4))
2.1.2 EWKT、EWKB和Canonical格式
PostGIS自身又在WKT和WKB基础上扩展实现了EWKT和EWKB来满足更复杂的场景需求,EWKT和EWKB相比OGC WKT和WKB格式主要的扩展有3DZ、3DM、4D坐标和内嵌空间参考支持。
2.1.3 SQL-MM格式
SQL-MM格式定义了一些插值曲线,这些插值曲线和EWKT有点类似,也支持3DZ、3DM、4D坐标,但是不支持嵌入空间参考。
2.2 地理类型(Geography Type)
地理类型提供支持本地空间特性的“地理”坐标(有时称为“大地”坐标,或“纬度/经度”,或“经度/纬度”)。它的几何基础是球面。
计算两点间的距离相当于计算圆弧的距离,不能使用平面几何原理,需要通过其他参考方法计算。
由于底层算法复杂,定义的地理类型比空间类型少很多,随之算法的增加,将出现新的地理类型。
PostGresSQL8.3推出一张表辅助空间参考表:spatial_ref_sys表,它存放的是OGC规范的空间参考。辅助转化。
地理类型只支持简单的简单的元素。标准几何类型数据将自动转换到地理WGS84坐标。还可以使用EWKT和EWKB约定来插入数据。
patial_ref_sys表,它存放的是OGC规范的空间参考。我们取我们最熟悉的4326参考看一下:
它的srid存放的就是空间参考的Well-Known ID,对这个空间参考的定义主要包括两个字段,srtext存放的是以字符串描述的空间参考,proj4text存放的则是以字符串描述的PROJ.4 投影定义(PostGIS使用PROJ.4实现投影)
SRID 4326声明了地理空间参考系统
如下创建表:
CREATE TABLE global_points ( id SERIAL PRIMARY KEY, name VARCHAR(64), location GEOGRAPHY(POINT,4326) );
插入数据:
INSERT INTO global_points (name, location) VALUES ('London', ST_GeographyFromText('SRID=4326; POINT(-72.1235 42.3521)'));
2.3 PostGIS对几何信息的检查
PostGIS可以检查几何信息的正确性,这主要是通过IsValid函数实现的。 以下语句分辨检查了2个几何对象的正确性,显然,(0, 0)点和(1,1)点可以构成一条线,但是(0, 0)点和(0, 0)点则不能构成,这个语句执行以后的得出的结果是TRUE,FALSE。
select IsValid('LINESTRING(0 0, 1 1)'), IsValid('LINESTRING(0 0,0 0)')
默认PostGIS并不会使用IsValid函数检查用户插入的新数据,因为这会消耗较多的CPU资源(特别是复杂的几何对象)。当你需要使用这个功能的时候,你可以使用以下语句为表新建一个检查约束:
ALTER TABLE cities ADD CONSTRAINT geometry_valid CHECK (IsValid(shape))
这时当我们往这个表试图插入一个错误的空间对象的时候,会得到一个错误:
INSERT INTO test.cities ( shape, name ) VALUES ( GeomFromText('LINESTRING(0 0,0 0)', 4326), '北京'); ERROR: new row for relation "cities" violates check constraint "geometry_valid" SQL 状态: 23514
三、PostGIS中的常用函数
3.1 图形和地理位置
- ST_GeometryType(geometry) —— 返回几何图形的类型
- ST_Transform(geometry, srid)——将几何图形投影为地理坐标数据 或 转换为不同srid坐标系统的坐标数据
- Geography(geometry)——将基于EPSG:4326(srid=4326)的geometry数据类型转换为geography数据类型
- ST_NDims(geometry) —— 返回几何图形的维数
- ST_SRID(geometry) —— 返回几何图形的空间参考标识码 srid
- ST_SetSRID(geometry,SRID)——设置srid
- sum(expression) ——返回一个计算式/表达式的和
- count(expression) ——返回一个表达式中的次数
PS : geometry,是几何类型的列的列名
srid,不同的srid就是不同标准的坐标系
点空间函数:
- ST_X(geometry) —— 返回X坐标
- ST_Y(geometry) —— 返回Y坐标
线串空间函数:
- ST_Length(geometry) —— 返回线串的长度
- ST_StartPoint(geometry) —— 将线串的第一个坐标作为点返回
- ST_EndPoint(geometry) —— 将线串的最后一个坐标作为点返回
- ST_NPoints(geometry) —— 返回线串的坐标数量
多边形空间函数:
- ST_Area(geometry) —— 返回多边形的面积
- ST_NRings(geometry) —— 返回多边形中环的数量(通常为1个,其他是孔)
- ST_ExteriorRing(geometry) —— 以线串的形式返回多边形最外面的环
- ST_InteriorRingN(geometry, n) —— 以线串形式返回指定的内部环
- ST_Perimeter(geometry) —— 返回所有环的长度
集合空间函数(多点、多线、多面、任意图形组合):
- ST_NumGeometries(geometry) —— 返回集合中的组成部分的数量
- ST_GeometryN(geometry, n) —— 返回集合中指定的组成部分
- ST_Area(geometry) —— 返回集合中所有多边形组成部分的总面积
- ST_Length(geometry) —— 返回所有线段组成部分的总长度
3.2 几何图形输入和输出
在数据库中,几何图形(Geometry)以仅供PostGIS使用的格式存储在磁盘上。为了让外部程序插入和检索有用的几何图形信息,需要将它们转换为其他应用程序可以理解的格式。
①Well-known text(WKT)
- ST_GeomFromText(text, srid) —— 返回geometry,除非指定SRID,否则将得到一个包含未知SRID的几何图形
- ST_GeographyFromText(text)——返回Geography
- ST_AsText(geometry) —— 返回text
- ST_AsEWKT(geometry) —— 返回text
②Well-known binary(WKB)
- ST_GeomFromWKB(bytea) —— 返回geometry
- ST_AsBinary(geometry) —— 返回bytea
- ST_AsEWKB(geometry) —— 返回bytea
③Geographic Mark-up Language(GML)
- ST_GeomFromGML(text) —— 返回geometry
- ST_ASGML(geometry) —— 返回text
④Keyhole Mark-up Language(KML)
- ST_GeomFromKML(text) —— 返回geometry
- ST_ASKML(geometry) —— 返回text
- ST_AsGeoJSON(geometry) —— 返回text
⑥Scalable Vector Graphics(SVG)
- ST_AsSVG(geometry) —— 返回text
以上函数最常见的用法是将几何图形的文本(text)表示形式转换为内部表示形式
请注意,除了具有几何图形表示形式的文本参数外,还可以指定一个提供几何图形SRID的数字参数。
3.3 图形关系
ST_Equals(geometry A, geometry B)
- 用于测试两个图形的空间相等性。
- 如果两个相同类型的几何图形具有相同的x、y坐标值,即如果第二个图形与第一个图形的坐标信息相等(相同),则ST_Equals()返回TRUE。
ST_Intersects、ST_Disjoint、ST_Crosses和ST_Overlaps
- ST_Intersects、ST_Crosses和ST_Overlaps测试几何图形是否相交。
- 如果两个图形有重合的部分,即如果它们的边界或内部相交,则**ST_Intersects(geometry A, geometry B)**返回TRUE
- ST_Disjoint(geometry A, geometry B),如果两个几何图形没有重合的部分,则它们不相交,反之亦然。事实上测试"not intersect"通常比测试"disjoint"更有效,因为intersect测试可以使用空间索引
- 对于multipoint/polygon、multipoint/linestring、linestring/linestring、linestring/polygon和linestring/multipolygon的比较,如果相交生成的几何图形的维度小于两个源几何图形的最大维度,且相交集位于两个源几何图形的内部,则**ST_Crosses(geometry A, geometry B)**将返回TRUE。
- **ST_Overlaps(geometry A, geometry B)比较两个相同维度**的几何图形,如果它们的结果集与两个源几何图形都不同但具有相同维度,则返回TRUE。
ST_Touches()
- 测试两个几何图形是否在它们的边界上接触,但在它们的内部不相交
- 如果两个几何图形的边界相交,或者只有一个几何图形的内部与另一个几何图形的边界相交,则**ST_Touches(geometry A, geometry B)**将返回TRUE
ST_Within和ST_Contains
- ST_Within()和ST_Contains()测试一个几何图形是否完全位于另一个几何图形内
- 如果第一个几何图形完全位于第二个几何图形内,则ST_Within(geometry A, geometry B)返回TRUE,ST_Within()测试的结果与ST_Contains()完全相反
- 如果第二个几何图形完全包含在第一个几何图形内,则ST_Contains(geometry A, geometry B)返回TRUE
ST_Distance和ST_DWithin
- **ST_Distance(geometry A, geometry B)**计算两个几何图形之间的最短距离,并将其作为浮点数返回。这对于实际报告几何图形之间的距离非常有用
- ST_DWithin(),测试两个几何图形之间的距离是否在某个范围之内,
3.4 geography类型
- ST_AsText(geography) returns
text - ST_GeographyFromText(text) returns
geography - ST_AsBinary(geography) returns
bytea - ST_GeogFromWKB(bytea) returns
geography - ST_AsSVG(geography) returns
text - ST_AsGML(geography) returns
text - ST_AsKML(geography) returns
text - ST_AsGeoJson(geography) returns
text - ST_Distance(geography, geography) returns
double - ST_DWithin(geography, geography, float8) returns
boolean - ST_Area(geography) returns
double - ST_Length(geography) returns
double - ST_Covers(geography, geography) returns
boolean - ST_CoveredBy(geography, geography) returns
boolean - ST_Intersects(geography, geography) returns
boolean - ST_Buffer(geography, float8) returns
geography[1] - ST_Intersection(geography, geography) returns
geography[1]
geography转换为geometry
PostgreSQL的类型转换语法是将 ::typename 附加到希望转换的值的末尾。因此,2::text将数字2转换为文本字符串"2";‘POINT(0 0)’ :: geometry将点的文本表示形式转换为geometry点
四、空间连接
空间连接(spatial joins)是空间数据库的主要组成部分,它们允许你使用空间关系作为连接键(join key)来连接来自不同数据表的信息,如:
SELECT subways.name AS subway_name, neighborhoods.name AS neighborhood_name, neighborhoods.boroname AS borough FROM nyc_neighborhoods AS neighborhoods JOIN nyc_subway_stations AS subways ON ST_Contains(neighborhoods.geom, subways.geom) WHERE subways.name = 'Broad St';
任何在两个表之间提供true/false关系的函数都可以用来驱动空间连接,但最常用的函数是:
ST_Intersects、ST_Contains和ST_DWithin
默认情况下,数据库使用的是INNER JOIN连接类型,还可以用 LEFT OUTER JOIN、RIGHT OUTER JOIN
五、空间索引
5.1 创建和使用索引
如下创建一个空间索引:
CREATE INDEX nyc_census_blocks_geom_idx ON nyc_census_blocks USING GIST (geom)
USING GIST子句告诉PostgreSQL在构建索引时使用generic index structure(GIST-通用索引结构)
PostGIS使用"R-Tree"空间索引结构。R-Tree将数据分解为矩形(rectangle)、子矩形(sub-rectangle)和子-子矩形(sub-sub rectangle)等。它是一种可自动处理可变数据的密度和对象大小的自调优(self-tuning)索引结构。
对于一个大的数据表来说,先计算出近似结果,然后进行精确测试的"两遍"机制可以从根本上减少计算量。(这种思想就是粗调和精调的思想,就像显微镜一样有粗粒度的调整和细粒度的调整。很多事物都涉及到这个思想,它的作用就是减少了耗费的代价)
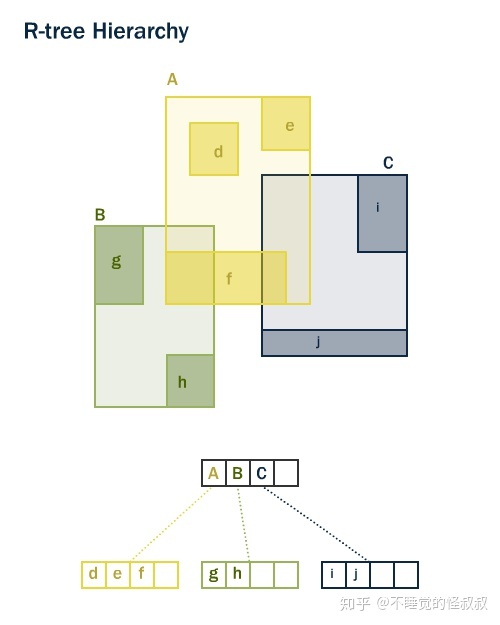
使用索引:
- 纯索引查询:使用"&&“运算符。对于几何图形,&&运算符表示"边界框重叠或接触”(纯索引查询),就像对于数字,"=“运算符表示"值相同”。
SELECT Sum(popn_total)FROM nyc_neighborhoods neighborhoodsJOIN nyc_census_blocks blocksON neighborhoods.geom && blocks.geomWHERE neighborhoods.name = 'West Village';
- PostGIS中最常用的函数(ST_Contains、ST_Intersects、ST_DWithin等)都包含自动索引过滤器
- 有些函数(如ST_Relate)不包括索引过滤器
5.2 分析(ANALYZE)
PostgreSQL查询规划器(query planner)智能地选择何时使用或不使用空间索引来计算查询。与直觉相反,执行空间索引搜索并不总是更快:如果搜索将返回表中的每条记录,则遍历索引树以获取每条记录实际上比从一开始线性读取整个表要慢(注意这句话)。
为了弄清楚要处理的数据的大概内容(读取表的一小部分信息,而不是读取表的大部分信息),PostgreSQL保存每个索引列中数据分布的统计信息。默认情况下,PostgreSQL定期收集统计信息。但是,如果你在短时间内更改了表的构成,则统计数据将不会是最新的。
为确保统计信息与表内容匹配,明智的做法是在表中加载和删除大容量数据后手动运行ANALYZE命令。这将强制统计系统收集所有索引列的统计信息。
ANALYZE命令要求PostgreSQL遍历该表并更新用于查询操作而估算的内部统计信息。
ANALYZE nyc_census_blocks;
5.3 清理(VACUUM)
值得强调的是,仅仅创建空间索引不足以让PostgreSQL有效地使用它。每当创建新索引或对表大量更新、插入或删除后,都必须执行清理(VACUUMing)。VACUUM命令要求PostgreSQL回收表页面中因记录的更新或删除而留下的任何未使用的空间。
清理对于数据库的高效运行非常关键,因此,PostgreSQL提供了一个“自动清理(autovacuum)"选项。
默认情况下,自动清理机制会根据活动级别确定的合理时间间隔自动清理(恢复空间)和分析(更新统计信息)。虽然这对于高度事务性的数据库是必不可少的功能,但在添加索引或大容量数据之后等待自动清理运行是不明智的,如果执行大批量更新,则应该手动运行VACUUM命令。
根据需要,可以单独执行清理和分析。发出VACUUM命令不会更新数据库统计信息;同样,执行ANALYZE命令也不会清理未使用的表空间。这两个命令都可以针对整个数据库、单个表或单个列运行。
VACUUM ANALYZE nyc_census_blocks;
六、几何图形创建函数
6.1 ST_Centroid / ST_PointOnSurface
- ST_Centroid(geometry) —— 返回大约位于输入几何图形的质心上的点。这种简单的计算速度非常快,但有时并不可取,因为返回点不一定在要素本身上。如果输入的几何图形具有凸性(假设字母’C’),则返回的质心可能不在图形的内部。
- ST_PointOnSurface(geometry) —— 返回保证在输入多边形内的点。从计算上讲,它比centroid操作代价要大得多。
6.2 ST_Buffer
**ST_Buffer(geometry, distance)**接受几何图形和缓冲区距离作为参数,并输出一个多边形,这个多边形的边界与输入的几何图形之间的距离与输入的缓冲区距离相等。
6.3 ST_Intersection
叠置(overlay)- 通过计算两个重叠多边形的交集来创建新的几何图形。
**ST_Intersection(geometry A, geometry B)**函数返回两个参数共有的空间区域(或直线,或点)。如果参数不相交,该函数将返回一个空几何图形
6.4 ST_Union
ST_Union将两个几何图形合并起来。ST_Union函数有两种形式
- ST_Union(geometry, geometry) —— 接受两个几何图形参数并返回合并的并集。
- ST_Union([geometry]) —— 接受一组几何图形并返回全部几何图形的并集。ST_Union([geometry])可与GROUP BY语句一起使用,以创建经过细致合并的基本几何图形集。这种操作非常强大。
七、图形有效性和简单性
- ST_IsValid(geometry),检查图形有效性
- 可以通过添加CHECK约束(即用户定义的完整性约束)来手动对表强制执行这样的有效性检查
- ST_IsValidReason(geometry),查找无效的原因
- ST_MakeValid,函数尝试在不对输入几何图形进行更改的情况下修复缺陷。不会删除或移动任何顶点,只需重新排列对象的结构即可。对于清晰但无效的数据来说,这个函数非常适用,对于杂乱无章且无效的数据来说,这个函数可能并不适用
- ST_IsSimple(),检查图形的简单性
- 几何图形的简单性可以理解为几何图形比较简单整齐,不会自己与自己重叠,不繁杂
7.1 点的简单性与有效性
7.1.1 单点
单个点(Point)肯定是简单的且有效的,因为一个点孤零零的肯定是简单、有效的
7.1.2 多点
多个点(MultiPoint)肯定是有效的,但不一定是简单的。
如果多点中有两个或两个以上的点重合(也就是坐标一致),那么它就不是简单的,但是确是有效的
7.2 线串的简单性与有效性
7.2.1 单线串
单线串(LINESTRING)如果有重叠、相交就不是简单的(除了端点相交,端点相交就说明这条线串是闭合的,但它是简单的)
7.2.2 多线串
多线串(MULTILINESTRING)只要它的元素(LINESTRING)都是简单的,且两个元素只在某个点相切,那么它就是简单
7.3 多边形的简单性与有效性
7.3.1 单多边形
有效性:
- 多边形的环必须闭合
- 内环应该处于外环的内部
- 环不能自相交(它们不能相互接触,也不能交叉)
- 环不能与其他环接触,除非在某个点相切(只能有一个在一个点相切)
多边形的环只要不自相交,则该多边形就是简单的
7.3.2 多多边形
多多边形里只要各个子元素(单多边形)是简单的、有效的,而且子元素之间只在有限的点上接触,那么它就是简单的、有效的。
八、几何图形的相等
8.1 精确相等(ST_OrderingEquals)
精确相等是通过按顺序逐个比较两个几何图形的顶点来确定的,以确保它们在位置上是相同的。确定图形的点位置和顺序不同,则图形不等
8.2 空间相等(ST_Equals)
精确的相等并没有考虑到几何图形的空间性质。有一个名为ST_Equals的函数,可用于测试几何图形的空间相等性或等价性。无论是绘制多边形的方向、定义多边形的起点,还是使用的点的个数的差异在这里都不重要。重要的是多边形包含相同的空间区域。图形的实际形状相同,则图形相等
8.3 等边界框(=)
在最坏的情况下,需要精确相等来比较几何图形中的每个顶点以确定相等。这可能会比较慢,并且可能不适合数量大的几何图形。为了更快地进行比较,提供了等边界运算符 ’ = ’ 。这仅在**边界框(矩形)**上操作,确保几何图形占用相同的二维范围,但不一定占用相同的空间。**边界框(矩形)**相同,则图形相等
九、最近领域搜索
执行最近邻域搜索的简单方法是按与要查询的几何图形的距离对候选表进行排序,然后获取最小距离对应的表记录
SELECT streets.gid, streets.nameFROM nyc_streets streets, nyc_subway_stations subwaysWHERE subways.name = 'Broad St'ORDER BY ST_Distance(streets.geom, subways.geom) ASCLIMIT 1;
十、其他函数
10.1 创建空栅格函数
ST_MakeEmptyRaster用于创建一个空的没有像元值的栅格(没有波段),各个参数用于定义这个空栅格的元数据:
- width、height —— 栅格的列数和行数
- upperleftx、upperlefty —— 对应空间坐标系中栅格左上角的坐标
- scalex、scaley —— 单个像元的宽度和长度(单位等同于空间参考坐标系的单位)。
- skewx、skewy —— 旋转角度,如果栅格数据北方朝上,该值为0。默认值为0。
- srid —— 空间参考坐标系,默认被设置为0。
- pixelsize —— 单个像元的宽度和长度。当scalex和scaley相等时,就可以直接使用这个参数设置像元大小。
上面的第一个函数签名传入现有的栅格数据作为新创建栅格的模板,会返回具有相同元数据(没有波段、没有像元值)的栅格数据。
在创建了一个空栅格之后,要向其添加波段,并可能要对其进行编辑。可以使用以下函数:
- ST_AddBand —— 用于定义波段。
- ST_SetValue —— 用于设置像元值
10.2 矢量切片坐标转换函数
ST_AsMVTGeom
将一个图层中位于参数box2d范围内的一个几何图形的所有坐标转换为MapBox VectorTile坐标空间里的坐标。
该函数会尽量保持、甚至纠正,来确保几何图形的有效性(有效性可以查看这篇文章:https://zhuanlan.zhihu.com/p/117267292),并可能在此过程中将几何图形降维(比如三维几何图形被处理成二维几何图形)。
函数各个参数的含义:
- geom —— 被转换的几何图形信息。
- bounds —— 某个矢量切片的范围对应的空间参考坐标系中的几何矩形框(没有缓冲区)。
- extent —— 是按规范定义的矢量切片坐标空间中的某个矢量切片的范围。如果为NULL,则默认为4096(边长为4096个单位的正方形)。
- buffer —— 矢量坐标空间中缓冲区的距离,位于该缓冲区的几何图形部位根据clip_geom参数被裁剪或保留。如果为NULL,则默认为256。
- clip_geom —— 用于选择位于缓冲区的几何图形部位是被裁剪还是原样保留。如果为NULL,则默认为true。
10.3 生成矢量切片的函数
ST_AsMVT聚合函数用于将基于MapBox VectorTile坐标空间的几何图形转换为MapBox VectorTile二进制矢量切片。
PostGIS生成MVT矢量切片的步骤是:
- 使用ST_AsMVTGeom函数将几何图形的所有坐标转换为MapBox VectorTile坐标空间里的坐标,这样就将基于空间坐标系的几何图形转换成了基于MVT坐标空间的几何图形。
- 使用ST_AsMVT函数将基于MVT坐标空间的几何图形转换为MVT二进制矢量切片。
MVT格式可以存储具有不同属性集的要素。要使用此功能,请在行数据中包含一个JSONB列,该列通过在一级深度下包含多个Json对象来存储多个不同属性集。JSONB中的键和值将被编码为要素属性。
可以通过"||"操作符调用多次这个函数来同时创建多个图层的同一位置的矢量切片。
**注意:**不要将GEOMETRYCOLLECTION类型的几何图形作为参数进行切片,但是可以使用ST_AsMVTGeom函数来准备GEOMETRYCOLLECTION类型的几何图形。
函数各个参数的含义:
- row —— 至少具有一个geometry列的行数据。
- name —— 图层名字,默认为"default"。
- extent —— 由MVT规范定义的屏幕空间(MVT坐标空间)中的矢量切片范围。
- geom_name —— row参数的行数据中geometry列的列名,默认是第一个geometry类型的列。
- feature_id_name —— 行数据中要素ID列的列名。如果未指定或为NULL,则第一个有效数据类型(smallint, integer, bigint)的列将作为要素ID列,其他的列作为要素属性列。
